Precios lineales con ruido - Regresión lineal vs Red neuronal
Problema
Supongamos unos datos de precios de vivienda en base a un solo parámetro: una distancia que va de 0 a 1.
Tenemos 100 datos reales que relacionan Distancia y Precio mostrados en la siguiente tabla y gráfica:
| DISTANCIA | PRECIO |
|---|---|
| 0,00 | 128300 |
| 0,01 | 128300 |
| 0,02 | 80691 |
| .... | ..... |
| .... | ..... |
| 0,98 | 190436 |
| 0,99 | 195652 |
| 1,00 | 228311 |
Planteamiento
Como podemos observar la nube de precios sigue un patrón lineal con cierto "ruido" creciendo el precio con la distancia. El problema pues se puede plantear como:
- Regresión lineal simple donde ajustamos una recta a la nube de datos. Azure ML nos ofrece 2 cálculos:
- Regresión no lineal donde ajustamos una curva que se adapte a la nube de datos. Azure ML ofrece "Regresión de Red Neuronal" donde configuramos una red neuronal para este objetivo y que se puede ver aquí.
Existe todo un curso completo de Machine Learning aquí.
Azure Machine Learning
Es una herramienta basada en servicios cloud que permite realizar todo el proceso de análisis de datos de forma sencilla como se puede ver aquí.
Crearemos 2 experimentos con 2 de los planteamientos citados y optimizaremos sus configuraciones para obtener los mejores resultados.
En ellos tomaremos las distancias / precios que existen entrenando a un subconjunto de datos para predecir el valor del resto. Esto generará un error entre el valor predicho y el real que trataremos de mejorar según la configuración de cada subexperimento.
Partiendo de unas configuraciones iniciales obtenemos la calidad de los modelos:
MÉTODO DE MÍNIMOS CUADRADOS
Nuestro experimento calcula la linea recta que mejor se ajusta a un 75% de nuestra nube de puntos generando un error de predicción sobre el resto.
Veamos el esquema - configuración - resultados
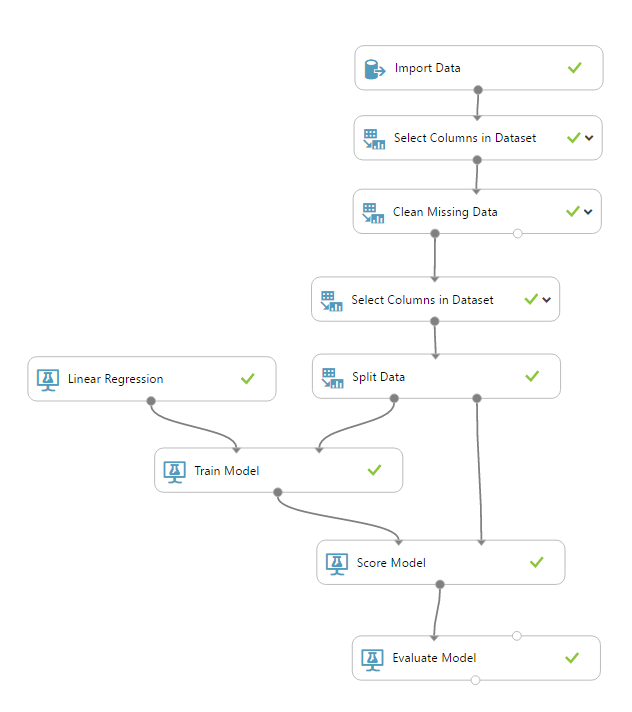

La configuración elegida se basa en:
- L2 regularization weight: Dejamos el valor por defecto para la regularización de los pesos en un sobreajuste, como se explica aquí y desde un punto de vista matemático aquí.
- Include intercept term: Es obvio que la recta entre precios y distancias debe cortar el eje a una cierta altura.
- Random number seed: Lo dejamos vacío puesto que no queremos mantener los mismos resultados al ejecutar nuevamente nuestro proyecto.
- Allow unknow categorical levels: Dejamos el valor por defecto, seleccionado, aunque en este caso no hay ningún precio nulo en los datos introducidos.
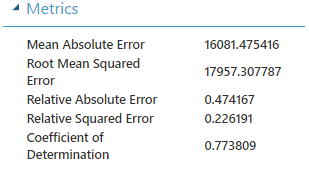
El resultado es que la Regresión lineal con el Método de mínimos cuadrados ordinarios nos deja un Coeficiente de Determinación (ver aquí) = 0.773809
REGRESIÓN POR RED NEURONAL
Nuestro experimento entrena con un 75% de los datos y comprueba la precisión de dicho entrenamiento con:
- El 25% restante.
- El mismo 75%. Esto se hace para detectar el sobreajuste del que hablaremos más adelante.
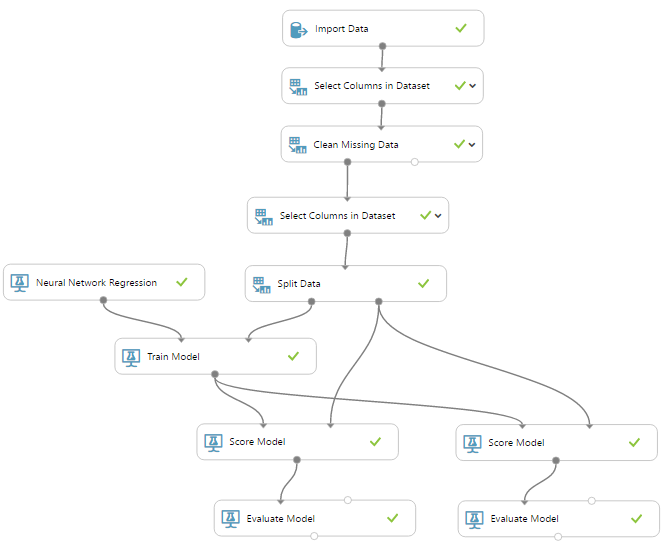
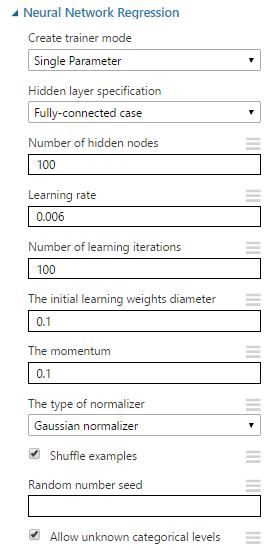
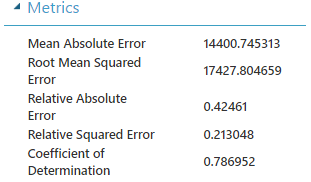
"Juguemos" con las distintas configuraciones de la red y su entrenamiento para obtener otros coeficientes de determinación (R2):
| Creater Training Mode | Hidden layer specification | Number of hidden nodes | Learning rate | Number of learning iterations | Initial learning weight | Momentum | Type of normalizer | Coeficiente de determinación |
|---|---|---|---|---|---|---|---|---|
| Single Parameter | Fully-connected case | 100 | 0,006 | 100 | 0.1 | 0.1 | Gaussian | 0,786952 |
| Single Parameter | Fully-connected case | 102 | 0,006 | 100 | 0.1 | 0.1 | Gaussian | 0,663372 |
| Single Parameter | Fully-connected case | 98 | 0,006 | 100 | 0.1 | 0.1 | Gaussian | 0,764834 |
| Single Parameter | Fully-connected case | 98 | 0,008 | 100 | 0.1 | 0.1 | Gaussian | 0,715826 |
| Single Parameter | Fully-connected case | 100 | 0,008 | 100 | 0.1 | 0.1 | Gaussian | 0,630218 |
| Single Parameter | Fully-connected case | 100 | 0,004 | 100 | 0.1 | 0.1 | Gaussian | 0,449265 |
| Single Parameter | Fully-connected case | 100 | 0,007 | 100 | 0.1 | 0.1 | Gaussian | 0,740706 |
| Single Parameter | Fully-connected case | 100 | 0,008 | 120 | 0.1 | 0.1 | Gaussian | 0,711450 |
| Single Parameter | Fully-connected case | 100 | 0,006 | 120 | 0.1 | 0.1 | Gaussian | 0,613479 |
| Single Parameter | Fully-connected case | 100 | 0,006 | 90 | 0.1 | 0.1 | Gaussian | 0,747638 |
| Single Parameter | Fully-connected case | 98 | 0,006 | 90 | 0.1 | 0.1 | Gaussian | 0,761415 |
| Single Parameter | Fully-connected case | 100 | 0,006 | 100 | 0.1 | 0.2 | Gaussian | 0,676800 |
| Single Parameter | Fully-connected case | 100 | 0,006 | 100 | 0.1 | 0.09 | Gaussian | 0,672099 |
| Single Parameter | Fully-connected case | 100 | 0,006 | 100 | 0.5 | 0.1 | Gaussian | 0,242066 |
| Single Parameter | Fully-connected case | 100 | 0,006 | 100 | 0.01 | 0.1 | Gaussian | -2,380000 |
| Single Parameter | Fully-connected case | 200 | 0,006 | 200 | 0.1 | 0.1 | Gaussian | 0,362436 |
| Single Parameter | Fully-connected case | 200 | 0,006 | 200 | 0.1 | 0.99 | Gaussian | xxx |
| Single Parameter | Fully-connected case | 200 | 0,006 | 400 | 0.1 | 0.1 | Gaussian | 0,458760 |
| Creater Training Mode | Custom definition - Net# | Learning rate | Number of learning iterations | Initial learning weight | Momentum | Type of normalizer | Coeficiente de determinación | |
| Single Parameter | input Data auto; hidden H1[100] from Data all; output VALOR[1] from H1 all; | 0.006 | 100 | 0.1 | 0.1 | Gaussian | 0.680794 | |
| Single Parameter | input Data auto; hidden H1[200] from Data all; output VALOR[1] from H1 all; | 0.006 | 100 | 0.1 | 0.1 | Gaussian | 0.069099 | |
| Single Parameter | input Data auto; hidden H1[400] from Data all; output VALOR[1] from H1 all; | 0.006 | 100 | 0.1 | 0.1 | Gaussian | 0.507965 | |
| Single Parameter | input Data auto; hidden H1[300] from Data all; output VALOR[1] from H1 all; | 0.006 | 100 | 0.1 | 0.1 | Gaussian | -0.307134 | |
| Single Parameter | input Data auto; hidden H1[250] from Data all; output VALOR[1] from H1 all; | 0.006 | 100 | 0.1 | 0.1 | Gaussian | -3.064412 | |
| Single Parameter | input Data auto; hidden H1[150] from Data all; output VALOR[1] from H1 all; | 0.005 | 100 | 0.1 | 0.1 | Gaussian | 0.573491 | |
| Single Parameter | input Data auto; hidden H1[98] from Data all; output VALOR[1] from H1 all; | 0.005 | 100 | 0.1 | 0.1 | Gaussian | 0.764317 | |
| Single Parameter | input Data auto; hidden H1[95] from Data all; output VALOR[1] from H1 all; | 0.005 | 100 | 0.1 | 0.1 | Gaussian | 0.715185 | |
| Single Parameter | input Data auto; hidden H1[97] from Data all; output VALOR[1] from H1 all; | 0.005 | 100 | 0.1 | 0.1 | Gaussian | 0.705737 | |
| Single Parameter | input Data auto; hidden H1[99] from Data all; output VALOR[1] from H1 all; | 0.005 | 100 | 0.1 | 0.1 | Gaussian | 0.812208 | |
| Single Parameter | input Data auto; hidden H1[99] from Data all; output VALOR[1] from H1 all; | 0.005 | 200 | 0.1 | 0.1 | Gaussian | 0.750725 | |
| Single Parameter | input Data auto; hidden H1[99] from Data all; output VALOR[1] from H1 all; | 0.005 | 160 | 0.1 | 0.1 | Gaussian | 0.76817 | |
| Single Parameter | input Data auto; hidden H1 auto from Data all; output VALOR auto from H1 all; | 0.005 | 100 | 0.1 | 0.1 | Gaussian | 0.719983 | |
| Single Parameter | input Data auto; hidden H1 auto from Data all; output VALOR auto from H1 all; | 0.005 | 200 | 0.1 | 0.1 | Gaussian | 0.699857 | |
| Single Parameter | input Data auto; hidden H1[99] from Data all; output VALOR[1] from H1 all; | 0.005 | 260 | 0.1 | 0.1 | Gaussian | 0.823814 | |
| Single Parameter | input Data auto; hidden H1[99] from Data all; output VALOR[1] linear from H1 all; | 0.005 | 260 | 0.1 | 0.1 | Gaussian | 0.740535 | |
| Single Parameter | input Data auto; hidden H1 auto from Data all; output VALOR auto from H1 all; | 0.005 | 80 | 0.1 | 0.1 | Gaussian | 0.717714 | |
Podemos conocer que significan los distintos parámetros de las configuraciones aquí. El mejor resultado con un Coeficiente de Determinación = 0.823814 lo encontramos en la fila marcada de color azul: red personalizada a una sola capa oculta de 99 neuronas con 260 iteraciones.
Pero, ¿que sistema predictivo hemos creado?
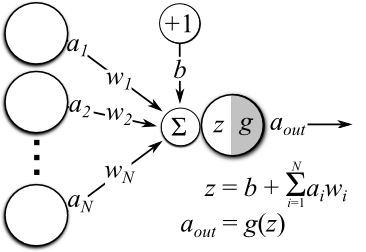
1. Cada neurona está haciendo su trabajo:
- El sumatorio de, multiplicar cada valor por un peso determinado (el inicial para la iteración 1) y sumarle un cierto número o umbral también denominado bias.
-
Al cálculo anterior asignarle una función de activación.
En nuestro caso al no especificarla Azure ML le asigna la función sigmoidal.
2.Entrenamiento:
Este lo definimos como una serie de iteraciones para reducir el error definido en la función de coste.
Aunque la función de coste más común es la del "Error cuadrático medio" Azure ML toma para este experimento "Cross Entropy" siendo ésta más óptima como se puede ver aquí.
Para calcular el mínimo de dicha función a base de iteraciones utilizamos el método descenso de gradiente.
Un proceso completo se puede ver aquí.
Conclusiones
La configuración de red neuronal:
| Creater Training Mode | Custom definition - Net# | Learning rate | Number of learning iterations | Initial learning weight | Momentum | Type of normalizer | Coeficiente de determinación | |
|---|---|---|---|---|---|---|---|---|
| Single Parameter | input Data auto; hidden H1[99] from Data all; output VALOR[1] from H1 all; | 0.005 | 260 | 0.1 | 0.1 | Gaussian | 0.823814 | |
mejora la predicción siendo el Coeficiente de Determinación R2=0.823814 frente al de la regresión lineal R2=0.773809.
Y para asegurarnos que no estamos sobreajustando el sistema si comparamos los precios entrenados 75% con ellos mismos obtenemos un Coeficiente de Determinación de R2=0.726789 así que no aparecen grandes diferencias.
El Coeficiente de Determinación es una medida del error en la predicción para regresiones lineales como se comprueba aquí que podemos extrapolar a la regresión en nuestro experimento.
Veamos en una gráfica animada e interactuando con los botones habilitados como se aproxima al valor óptimo de R2 en sucesivas iteraciones de entrenamiento:
- Coeficiente de Determinación Regresión Lineal
- Número de Iteraciones Entrenamiento
- Coeficiente de Determinación Red Neuronal
Resumen
Para realizar una aproximación a una estimación de precios en la comunidad de Madrid hemos generado un sistema con precios falsos que solo dependen de una variable distancia.
En este sistema simplificado y con ayuda de Azure ML la regresión no lineal mediante una red neuronal mejora la predicción alcanzando un Coeficiente de Determinación R2=0.823814 frente al de la regresión lineal R2=0.773809.
En el siguiente capítulo reconfiguraremos tanto la red como los parámetros de entrenamiento generando un sistema predictivo para precios reales tomados de los principales portales inmobiliarios en esta zona.