PRECIOS COMUNIDAD DE MADRID - Red Neuronal
Estructura
Siguiendo los pasos del capítulo anterior creamos un experimento simple con la siguiente estructura:
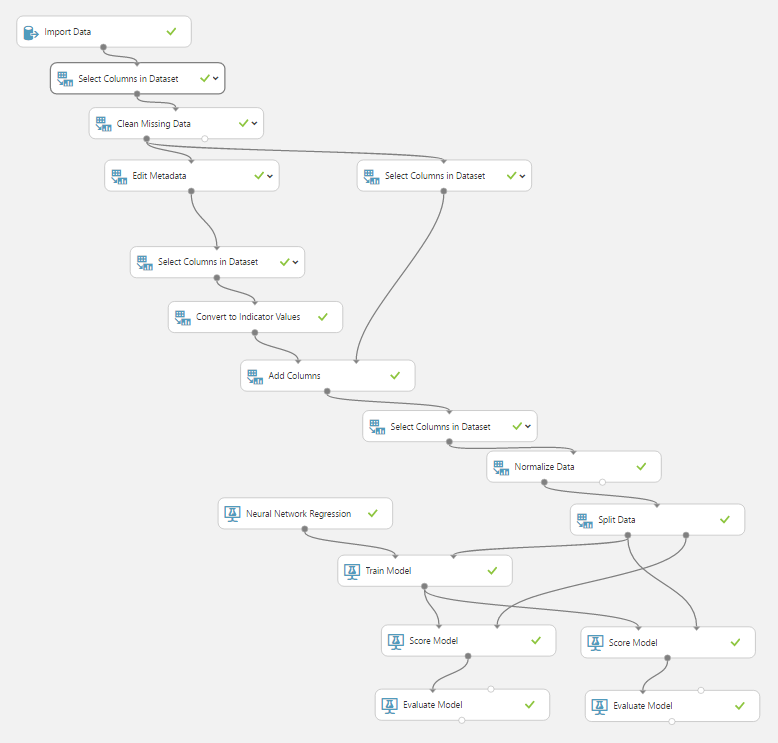

Módulos
Aunque los datos son escogidos por contener las 17 variables establecidas el experimento no debe añadir viviendas donde falte alguna de ellas. Para ello añadiremos a nuestra red el modulo "Clean missing data" eliminando cualquier fila (vivienda) donde falte el valor de alguna columna (parámetro).
Por otra parte haremos "categóricos" mediante el módulo "Edit Metadata (Make Categorical)" parámetros con valores discretos como número de baños, altura, tipo de inmueble.
Por ejemplo el número de Garajes se "expande" a 3 nuevos parámetros booleanos "Garaje_0", "Garaje 1", "Garaje 2" siendo las triadas posibles (1,0,0), (0,1,0) y (0,0,1).
Aplicando este razonamiento obtenemos 82 parámetros en los que el sistema debe basar su predicción.
Y por último agregamos al precio una normalización con el método de transformación MinMax reescalándolos al intervalo (0,1) como se puede ver aquí. Recordemos que la función de activación en las neuronas será la función sigmoide cuya curva tiene 2 asíntotas horizontales en 0 y 1.
Primeras conclusiones
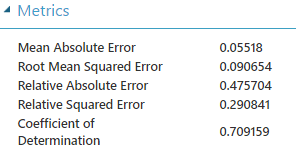
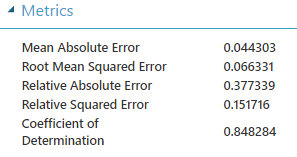
Se ha utilizado una capa con 164 nodos ocultos a un "ritmo" de 0.001 learning rate y con 1000 iteraciones. Los resultados miden la predicción de un grupo de 25% en base al 75% restante. Se lleva a cabo en unos 22 minutos aproximadamente dejando un Coeficiente de Determinación:
- 0.709159 para la predicción del 25%
- 0.848284 para la predicción del 75%
Claramente el sistema está sobreajustando los valores conocidos (75%) sobre aquellos que trata de predecir.
Tuneado de hyperparametros
Para saber que parametros generan una mejor predicción Azure ML provee una forma de entrenar el sistema para varias combinaciones de "learning Rate" e iteraciones, más información se puede encontrar aquí.
Entrenaremos nuestro sistema de 1 sola capa oculta con100 neuronas combinado los siguientes valores:
- "Learning rate": 0.025, 0.01, 0.02, 0.04, 0.05, 0.1, 0.4
- Iteraciones: 10, 20, 40, 80, 100, 160, 200, 250, 300, 350, 400, 500, 1000
Esto nos lleva al siguiente experimento:
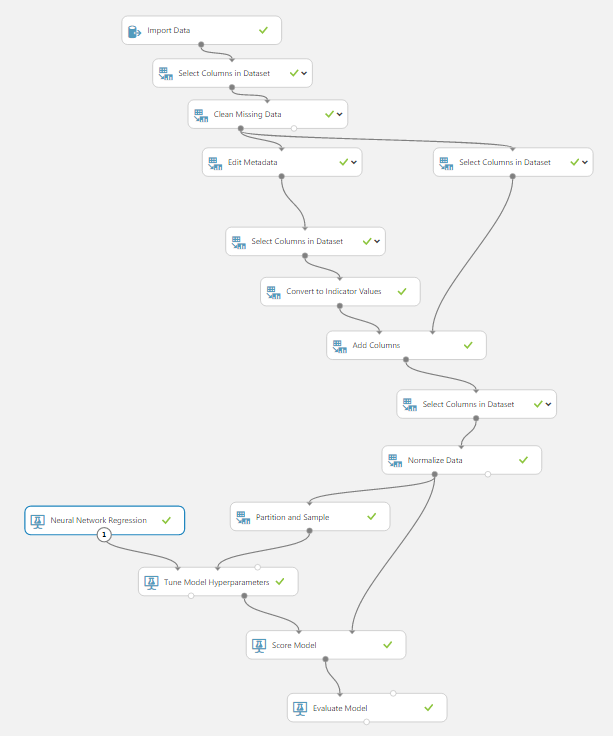
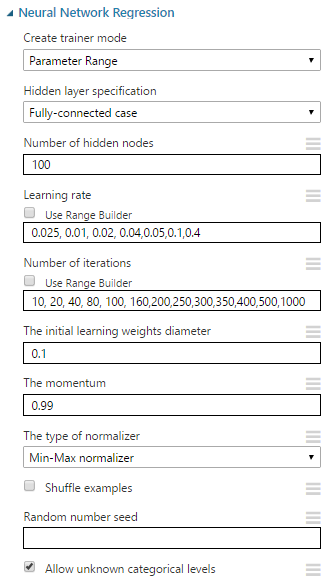
Después de más de 35 horas de entrenamiento sobre todas las combinaciones posibles los 100 primeros resultados se muestran en la siguiente tabla:
| LEARNING RATE | LOSS FUNCTION | ITERATIONS | MEAN ABSOLUTE ERROR | ROOT MEAN SQUARED ERROR | RELATIVE ABSOLUTE ERROR | RELATIVE SQUARED ERROR | COEFFICIENT OF DETERMINATION |
|---|---|---|---|---|---|---|---|
| 0.01 | CrossEntropy | 1000 | 0.095338 | 0.149832 | 0.814951 | 0.78008 | 0.21992 |
| 0.01 | CrossEntropy | 500 | 0.091736 | 0.143566 | 0.784165 | 0.716206 | 0.283794 |
| 0.01 | SquaredError | 160 | 0.091648 | 0.125478 | 0.783409 | 0.547105 | 0.452895 |
| 0.01 | SquaredError | 350 | 0.090878 | 0.131967 | 0.776833 | 0.605146 | 0.394854 |
| 0.01 | CrossEntropy | 100 | 0.090466 | 0.127191 | 0.773311 | 0.56214 | 0.43786 |
| 0.01 | CrossEntropy | 300 | 0.089878 | 0.133328 | 0.768281 | 0.617693 | 0.382307 |
| 0.01 | SquaredError | 400 | 0.089173 | 0.131459 | 0.762258 | 0.600503 | 0.399497 |
| 0.01 | SquaredError | 350 | 0.087847 | 0.131664 | 0.750921 | 0.602374 | 0.397626 |
| 0.01 | CrossEntropy | 160 | 0.087458 | 0.12368 | 0.747594 | 0.531538 | 0.468462 |
| 0.01 | SquaredError | 500 | 0.087286 | 0.13622 | 0.746123 | 0.64478 | 0.35522 |
| 0.01 | CrossEntropy | 200 | 0.085885 | 0.127221 | 0.734148 | 0.56241 | 0.43759 |
| 0.01 | CrossEntropy | 350 | 0.085488 | 0.134671 | 0.730759 | 0.630207 | 0.369793 |
| 0.01 | SquaredError | 500 | 0.084521 | 0.137844 | 0.722492 | 0.660253 | 0.339747 |
| 0.01 | CrossEntropy | 500 | 0.084456 | 0.134094 | 0.721934 | 0.624813 | 0.375187 |
| 0.01 | SquaredError | 250 | 0.084194 | 0.124636 | 0.719695 | 0.539779 | 0.460221 |
| 0.01 | SquaredError | 350 | 0.084176 | 0.130507 | 0.719541 | 0.591835 | 0.408165 |
| 0.01 | CrossEntropy | 300 | 0.083757 | 0.125249 | 0.715956 | 0.545103 | 0.454897 |
| 0.01 | CrossEntropy | 350 | 0.083232 | 0.131243 | 0.711475 | 0.59853 | 0.40147 |
| 0.01 | CrossEntropy | 1000 | 0.083068 | 0.139762 | 0.710066 | 0.678755 | 0.321245 |
| 0.01 | CrossEntropy | 1000 | 0.082989 | 0.141212 | 0.709391 | 0.692903 | 0.307097 |
| 0.01 | SquaredError | 1000 | 0.082964 | 0.143291 | 0.709182 | 0.713465 | 0.286535 |
| 0.01 | CrossEntropy | 1000 | 0.082741 | 0.135372 | 0.707276 | 0.636778 | 0.363222 |
| 0.01 | CrossEntropy | 200 | 0.082628 | 0.120574 | 0.706306 | 0.505176 | 0.494824 |
| 0.01 | SquaredError | 400 | 0.082228 | 0.131574 | 0.702893 | 0.601553 | 0.398447 |
| 0.01 | CrossEntropy | 250 | 0.082097 | 0.125316 | 0.701769 | 0.54569 | 0.45431 |
| 0.01 | SquaredError | 1000 | 0.082058 | 0.139622 | 0.701436 | 0.67739 | 0.32261 |
| 0.01 | CrossEntropy | 400 | 0.081693 | 0.132466 | 0.69832 | 0.609731 | 0.390269 |
| 0.01 | SquaredError | 100 | 0.08161 | 0.117662 | 0.69761 | 0.481065 | 0.518935 |
| 0.01 | CrossEntropy | 300 | 0.081531 | 0.129365 | 0.696934 | 0.581518 | 0.418482 |
| 0.01 | CrossEntropy | 200 | 0.081211 | 0.120498 | 0.694197 | 0.504538 | 0.495462 |
| 0.01 | CrossEntropy | 350 | 0.081009 | 0.122211 | 0.692467 | 0.518978 | 0.481022 |
| 0.01 | CrossEntropy | 500 | 0.080558 | 0.128152 | 0.688611 | 0.570671 | 0.429329 |
| 0.01 | CrossEntropy | 250 | 0.080478 | 0.123144 | 0.687933 | 0.526933 | 0.473067 |
| 0.01 | SquaredError | 400 | 0.080248 | 0.125298 | 0.68596 | 0.545529 | 0.454471 |
| 0.01 | SquaredError | 500 | 0.080105 | 0.1317 | 0.684739 | 0.602707 | 0.397293 |
| 0.01 | SquaredError | 300 | 0.080084 | 0.123449 | 0.68456 | 0.529551 | 0.470449 |
| 0.01 | CrossEntropy | 1000 | 0.079951 | 0.132682 | 0.683429 | 0.61172 | 0.38828 |
| 0.01 | SquaredError | 350 | 0.079697 | 0.130685 | 0.681252 | 0.59345 | 0.40655 |
| 0.01 | SquaredError | 1000 | 0.079587 | 0.142014 | 0.680318 | 0.700797 | 0.299203 |
| 0.01 | CrossEntropy | 400 | 0.079277 | 0.133453 | 0.677665 | 0.618851 | 0.381149 |
| 0.01 | CrossEntropy | 100 | 0.079038 | 0.112146 | 0.675625 | 0.437021 | 0.562979 |
| 0.01 | CrossEntropy | 500 | 0.0784 | 0.129538 | 0.67017 | 0.583076 | 0.416924 |
| 0.01 | SquaredError | 1000 | 0.078189 | 0.1343 | 0.668365 | 0.626738 | 0.373262 |
| 0.01 | SquaredError | 100 | 0.077481 | 0.111178 | 0.662308 | 0.42951 | 0.57049 |
| 0.01 | CrossEntropy | 300 | 0.077425 | 0.124458 | 0.66183 | 0.538238 | 0.461762 |
| 0.01 | CrossEntropy | 160 | 0.077313 | 0.116528 | 0.660874 | 0.471833 | 0.528167 |
| 0.01 | SquaredError | 1000 | 0.077201 | 0.136838 | 0.659916 | 0.65065 | 0.34935 |
| 0.01 | CrossEntropy | 350 | 0.07647 | 0.12267 | 0.653666 | 0.522887 | 0.477113 |
| 0.01 | SquaredError | 300 | 0.076263 | 0.123556 | 0.651903 | 0.53047 | 0.46953 |
| 0.01 | CrossEntropy | 250 | 0.076245 | 0.118407 | 0.651747 | 0.487175 | 0.512825 |
| 0.01 | SquaredError | 1000 | 0.076093 | 0.13975 | 0.65045 | 0.678636 | 0.321364 |
| 0.01 | SquaredError | 80 | 0.075747 | 0.108575 | 0.647492 | 0.409629 | 0.590371 |
| 0.01 | CrossEntropy | 400 | 0.075596 | 0.120673 | 0.646197 | 0.506003 | 0.493997 |
| 0.01 | SquaredError | 350 | 0.075584 | 0.124981 | 0.646092 | 0.542775 | 0.457225 |
| 0.01 | CrossEntropy | 400 | 0.075483 | 0.123514 | 0.645237 | 0.530107 | 0.469893 |
| 0.01 | CrossEntropy | 250 | 0.075279 | 0.118482 | 0.643489 | 0.48779 | 0.51221 |
| 0.01 | SquaredError | 160 | 0.075195 | 0.118578 | 0.642772 | 0.488583 | 0.511417 |
| 0.01 | CrossEntropy | 200 | 0.07514 | 0.114988 | 0.6423 | 0.45945 | 0.54055 |
| 0.01 | CrossEntropy | 500 | 0.07508 | 0.126966 | 0.64179 | 0.560152 | 0.439848 |
| 0.01 | SquaredError | 300 | 0.074821 | 0.119559 | 0.639572 | 0.496701 | 0.503299 |
| 0.01 | SquaredError | 300 | 0.074776 | 0.123761 | 0.639187 | 0.532233 | 0.467767 |
| 0.01 | CrossEntropy | 160 | 0.074762 | 0.113121 | 0.63907 | 0.444652 | 0.555348 |
| 0.01 | SquaredError | 400 | 0.074751 | 0.124131 | 0.638972 | 0.535419 | 0.464581 |
| 0.01 | SquaredError | 400 | 0.074717 | 0.125199 | 0.638686 | 0.544672 | 0.455328 |
| 0.01 | CrossEntropy | 1000 | 0.074465 | 0.137844 | 0.636531 | 0.660244 | 0.339756 |
| 0.01 | CrossEntropy | 80 | 0.074414 | 0.106267 | 0.636096 | 0.3924 | 0.6076 |
| 0.01 | CrossEntropy | 250 | 0.07405 | 0.1177 | 0.632985 | 0.481375 | 0.518625 |
| 0.01 | SquaredError | 350 | 0.07398 | 0.125697 | 0.632385 | 0.549016 | 0.450984 |
| 0.01 | CrossEntropy | 200 | 0.073976 | 0.116791 | 0.632348 | 0.473968 | 0.526032 |
| 0.01 | SquaredError | 350 | 0.073843 | 0.125235 | 0.631217 | 0.544986 | 0.455014 |
| 0.01 | SquaredError | 200 | 0.073776 | 0.11622 | 0.630643 | 0.469348 | 0.530652 |
| 0.01 | SquaredError | 250 | 0.073742 | 0.121841 | 0.630354 | 0.515847 | 0.484153 |
| 0.01 | SquaredError | 250 | 0.073661 | 0.114273 | 0.629662 | 0.453752 | 0.546248 |
| 0.01 | CrossEntropy | 250 | 0.073563 | 0.116138 | 0.628821 | 0.468686 | 0.531314 |
| 0.01 | SquaredError | 200 | 0.072985 | 0.114587 | 0.623882 | 0.456247 | 0.543753 |
| 0.01 | SquaredError | 400 | 0.072921 | 0.120874 | 0.623336 | 0.507688 | 0.492312 |
| 0.01 | CrossEntropy | 200 | 0.072762 | 0.113827 | 0.621976 | 0.450218 | 0.549782 |
| 0.01 | SquaredError | 160 | 0.072693 | 0.112925 | 0.621381 | 0.443111 | 0.556889 |
| 0.01 | CrossEntropy | 400 | 0.072669 | 0.126272 | 0.621174 | 0.55405 | 0.44595 |
| 0.01 | SquaredError | 1000 | 0.072666 | 0.136194 | 0.621151 | 0.644538 | 0.355462 |
| 0.01 | CrossEntropy | 100 | 0.072559 | 0.1058 | 0.620241 | 0.388957 | 0.611043 |
| 0.01 | SquaredError | 500 | 0.072144 | 0.12167 | 0.616688 | 0.5144 | 0.4856 |
| 0.01 | SquaredError | 80 | 0.072106 | 0.10593 | 0.616368 | 0.389911 | 0.610089 |
| 0.01 | SquaredError | 300 | 0.072076 | 0.115907 | 0.616109 | 0.466819 | 0.533181 |
| 0.01 | CrossEntropy | 500 | 0.072074 | 0.12531 | 0.616092 | 0.545634 | 0.454366 |
| 0.01 | SquaredError | 250 | 0.071845 | 0.117596 | 0.614136 | 0.480523 | 0.519477 |
| 0.01 | CrossEntropy | 250 | 0.07183 | 0.116362 | 0.614009 | 0.470492 | 0.529508 |
| 0.01 | SquaredError | 500 | 0.071815 | 0.127531 | 0.613879 | 0.565147 | 0.434853 |
| 0.01 | SquaredError | 250 | 0.071795 | 0.120771 | 0.61371 | 0.506823 | 0.493177 |
| 0.01 | CrossEntropy | 300 | 0.071784 | 0.121589 | 0.613611 | 0.513712 | 0.486288 |
| 0.01 | SquaredError | 400 | 0.071718 | 0.120629 | 0.613051 | 0.505631 | 0.494369 |
| 0.01 | SquaredError | 160 | 0.07152 | 0.111994 | 0.611353 | 0.435837 | 0.564163 |
| 0.01 | SquaredError | 160 | 0.071393 | 0.111835 | 0.610272 | 0.434596 | 0.565404 |
| 0.01 | SquaredError | 80 | 0.0711 | 0.10767 | 0.607768 | 0.402827 | 0.597173 |
| 0.01 | CrossEntropy | 1000 | 0.070783 | 0.131184 | 0.60506 | 0.59799 | 0.40201 |
| 0.01 | CrossEntropy | 10 | 0.070697 | 0.100687 | 0.604322 | 0.352274 | 0.647726 |
| 0.01 | CrossEntropy | 100 | 0.070158 | 0.108076 | 0.599714 | 0.405871 | 0.594129 |
| 0.01 | CrossEntropy | 350 | 0.070145 | 0.120942 | 0.5996 | 0.508262 | 0.491738 |
| 0.01 | SquaredError | 80 | 0.070004 | 0.105582 | 0.598397 | 0.38736 | 0.61264 |
| 0.01 | CrossEntropy | 160 | 0.069888 | 0.110935 | 0.597407 | 0.427634 | 0.572366 |
El resultado con mejor predicción para una capa oculta de 100 neuronas, un "initial weight diameter" de 0.1 y "momentum" 0.99 se produce para:
- "Learning rate": 0.01
- Iteraciones: 20
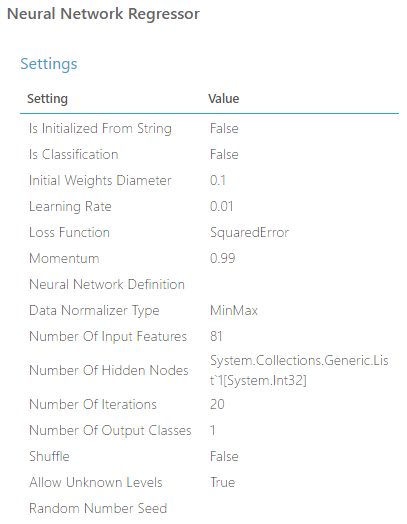
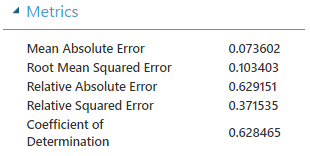
Observamos que el Coeficiente de determinación = 0.628465, un peor resultado que el experimento inicial. Esto es debido a que el número de neuronas por capa es 100 mientras que en el experimento inicial las fijamos a 164, 2 veces el número de parámetros de entrada, lo que suele ser un valor muy utilizado para conseguir mejores predicciones.
En un futuro pues sería bueno probar las combinaciones con 164 neuronas en la capa oculta y ver si mejoran las predicciones.
Optimización personalizada
Generaremos ahora una estructura neuronal con más de 1 capa oculta, menos iteraciones, y observaremos los nuevos resultados:
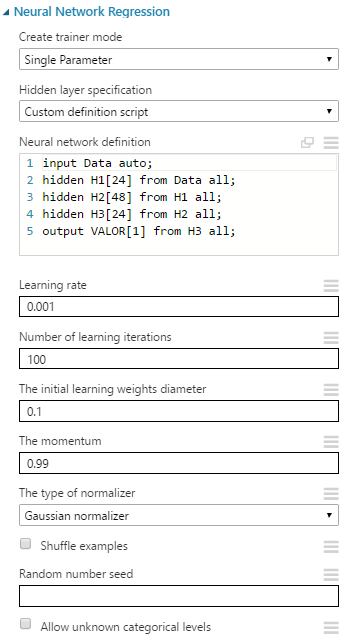
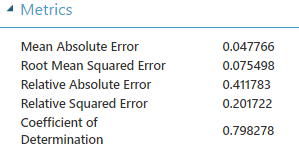

Los nuevos Coeficiente de Determinación:
- 0.798278 para la predicción del 25%
- 0.869896 para la predicción del 75%
Hemos mejorado el sistema inicial aunque seguimos teniendo cierto sobreajuste.
Generemos más neuronas por capas:
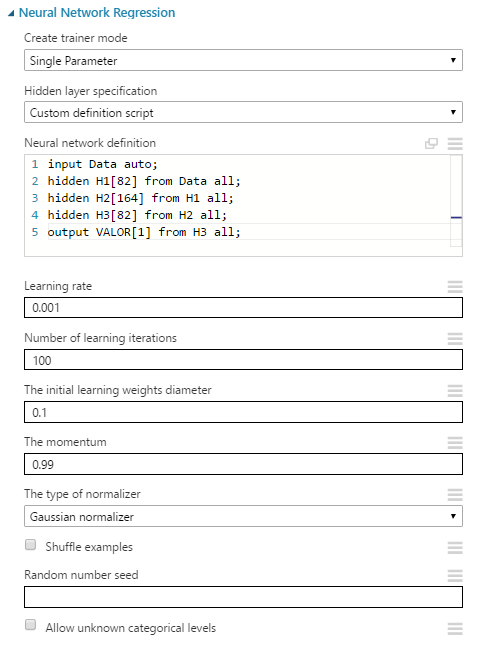
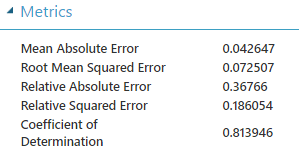
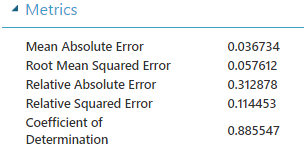
En un entrenamiento de poco más de 3 minutos el sobreajuste continúa pero mejoramos el Coeficiente de Determinación:
- 0.813946 para la predicción del 25%
- 0.885547 para la predicción del 75%
"Juguemos" con las iteraciones y comparemos los resultados:
| Iteraciones | Coeficiente de Determinación 25% | Coeficiente de Determinación 75% | Tiempo Entrenamiento |
|---|---|---|---|
| 20 | 0.757224 | 0.793305 | 2.5 min. |
| 40 | 0.800509 | 0.845398 | 2.5 min. |
| 50 | 0.814861 | 0.860217 | 2.75 min. |
| 100 | 0.813946 | 0.885547 | 3 min. |
| 150 | 0.798084 | 0.898534 | 4.5 min |
| 200 | 0.794861 | 0.908892 | 4.5 min. |
Podemos ver que logicamente el sistema se sobreajusta con mayor número de iteraciones. En las 50 iteraciones aproximadamente no tenemos un sobreajuste que prediga los datos testeados (25%) de forma errónea, algo que sí sucede con p.e. 150 iteraciones. Este dato pues es el más óptimo para la estructura de capas elegida con un coeficiente de determinación en torno a 0.81.